In alcuni ambienti del coseno del positivo? In alcuni ambienti di seno e coseno del positivo?
Questioni che sorgono nello studio delle funzioni trigonometriche sono diversi. Alcuni di loro – che quarti pubblici coseno positivo e negativo, in alcuni quartieri sine positivi e negativi. Tutto è facile se si sa come calcolare il valore di queste funzioni nei diversi angoli e familiarità con il principio di costruzione delle funzioni sul grafico.
Qual è il coseno
Se consideriamo il triangolo rettangolo, abbiamo la seguente rapporto aspetto che definisce: il coseno dell'angolo a è il rapporto della gamba adiacente l'ipotenusa BC AB (Figura 1): Cos a = BC / AB.
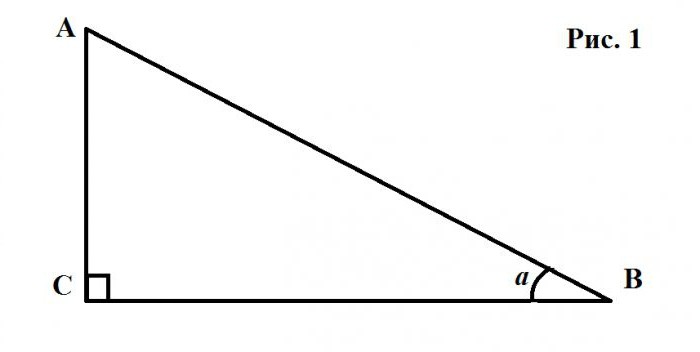
Con l'aiuto dello stesso triangolo, potete trovare il seno dell'angolo, la tangente e cotangente. La sinusite è il rapporto tra la gamba opposta verso l'angolo degli altoparlanti per l'ipotenusa AB. La tangente dell'angolo è, se l'angolo desiderato del seno diviso per il coseno dello stesso angolo; sostituendo la formula corrispondente trovare il coseno e seno, si ottiene che un tg = AC / BC. Cotangente è l'inverso della funzione tangente, sarà così: CTG a = BC / AC.
Cioè, si è trovato che è sempre lo stesso in un giusto rapporto triangolo aspetto per gli stessi valori dell'angolo. Sembrerebbe che era chiaro da questi valori, ma perché è un numero negativo?
Per fare questo, considerare il triangolo in un sistema di coordinate cartesiane, dove ci sono valori sia positivi che negativi.
Chiaramente circa un quarto, dove alcuni
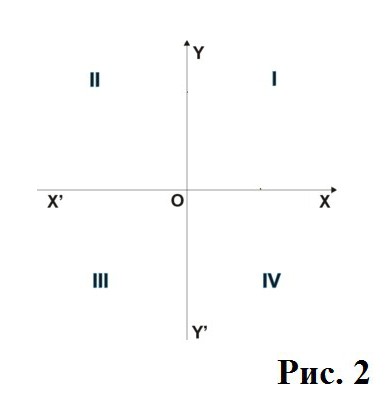Che cosa è coordinate cartesiane? Se parliamo spazio bidimensionale, abbiamo due linee dirette che si intersecano in un punto O – è l'asse x (Ox) e l'asse y (Oy). Dal punto O nella direzione di una linea retta sono collocati numeri positivi, ma nella direzione opposta – negativo. Da questo, alla fine, dipende direttamente, in qualsiasi quarti coseno è positiva, e in cui, di conseguenza, non.
primo trimestre
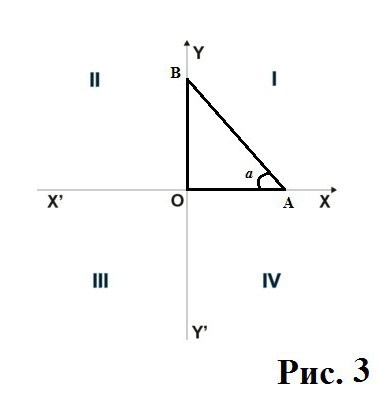
Se si inserisce un triangolo rettangolo nel primo trimestre (da 0 a 90), in cui l'asse xe y sono valori positivi (segmenti AO e BO sono sugli assi dove i valori sono segno "+"), allora quel peccato, che il coseno dello stesso avranno valori positivi, e sono assegnati un valore con un "plus". Ma cosa succede se si sposta il triangolo nel secondo trimestre (da 90 a 180)?
secondo trimestre
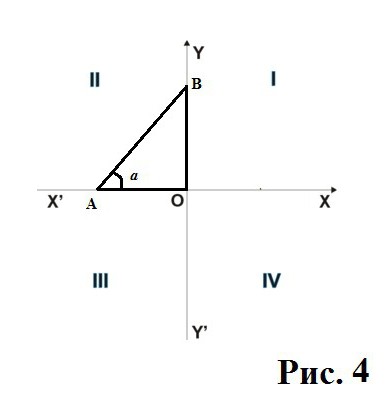
Vediamo che la gamba asse y JSC ricevuto un valore negativo. Il coseno dell'angolo ora ha un rapporto nel lato meno con, e quindi il suo valore finale diventa negativo. Risulta che il grado in cui un quarto del coseno è positivo dipende dalla posizione del triangolo nel sistema di coordinate cartesiane. E in questo caso, il coseno dell'angolo ottiene un valore negativo. Ma nulla è cambiato per il seno, al fine di determinare il segno della OB giusta direzione, che è rimasto in questo caso con un segno più. Per riassumere i primi due quarti.
Per scoprire in che quartieri Cosine pubblico positivi e negativi (così come del seno e altre funzioni trigonometriche), è necessario guardare a ciò che il segno assegnato ad uno o l'altro di una gamba. Per il coseno dell'angolo critico una gamba AB, per il seno – RH.
Il primo trimestre finora è stato l'unico a rispondere alla domanda: "In che quarti del seno e coseno positivo allo stesso tempo?". Guarda su, vero partite ancora il segno delle due funzioni.
Nel ritorno dei quarti JSC ha cominciato ad avere un valore negativo, e quindi il coseno è diventato negativo. Per un seno valore positivo memorizzato.
terzo trimestre
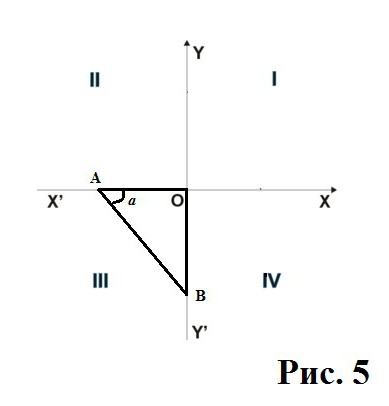
Ora entrambi gamba AB e OB è diventata negativa. Ricordiamo le relazioni per il seno e coseno:
Cos a = AB / AB;
Sin a = VO / AB.
AB ha sempre un segno positivo in questo sistema di coordinate, in quanto non è diretto a qualsiasi dei due assi di alcune parti. Ma le gambe diventano negativi, e quindi il risultato per entrambe le funzioni, anche negative, perché se si esegue la moltiplicazione o divisione con i numeri, tra cui uno e solo uno ha un segno "meno", il risultato sarà anche familiarità con questo.
Il risultato in questa fase:
1) In quale trimestre coseno positivo? Nella prima delle tre.
2) In quale quartiere sine positivo? Il primo e il secondo dei tre.
Il quarto trimestre (da circa 270 a circa 360)
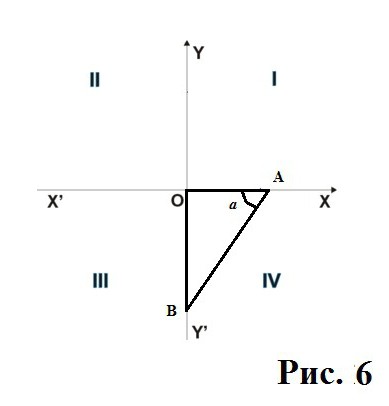
Qui gamba riacquista JSC segno "più", e quindi il coseno troppo.
Per il caso del seno è ancora "negativo" perché la gamba RH rimasto al di sotto del punto di partenza O.
risultati
Per comprendere in che quarti il coseno positivo, negativo, ecc, necessario ricordare il rapporto per calcolare il coseno: adiacente l'angolo della gamba divisa per l'ipotenusa. Alcuni insegnanti offrono così ricordare: a (osinus) = (a) calcio d'angolo. Se vi ricordate il "barare", che saprà automaticamente che il seno – è il rapporto tra la gamba opposta all'angolo per l'ipotenusa.
Ricordate, in ogni quartiere del coseno del pubblico positivo e negativo è abbastanza difficile. Funzioni trigonometriche molto, e tutti hanno il loro valore. Eppure, come risultato: per valori positivi di seno – 1, 2-quarto (da 0 a 180); per il coseno di 1, 4-quarto (da 0 a circa 90 e da circa 270 a circa 360). Nei restanti quarti delle funzioni sono definite con un meno.
Forse qualcuno sarà più facile da ricordare dove un cartello sulla funzione di immagine.
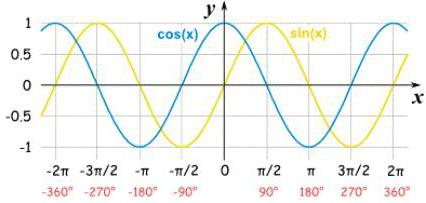
Per sinusale può essere visto che da zero a 180 sulla cresta supera linea valore sin (x), significa che la funzione è positivo. Per coseno così: in un quarto coseno positivo (figura 7), ed in cui si vede uno spostamento negativo sulle linee sopra e sotto l'asse di cos (x). Di conseguenza, possiamo ricordare sono due modi per determinare il segno della funzioni seno, coseno:
1. cerchio immaginario con raggio uguale a uno (anche se, in effetti, non importa quale il raggio del cerchio, ma nei libri di testo spesso portano solo un esempio, questo facilita la percezione, ma allo stesso tempo, a meno che sia non importa, i bambini possono confondersi).
2. Nell'immagine, a seconda della funzione (s) dall'argomento x come ultima figura.
Con il primo metodo può essere compreso da ciò che è firmare dipendente, e abbiamo spiegato in dettaglio sopra. Figura 7, costruita secondo questi dati al meglio rende la funzione risultante e la sua znakoprinadlezhnost.
