Come risolvere il quadrato magico (grado 3)? Vantaggi per gli studenti

enigmi matematici esistono numero inimmaginabile. Ciascuno di loro sono unici a modo loro, ma il loro fascino sta nel fatto che la soluzione dovrà inevitabilmente venire alle formule. Naturalmente, possiamo provare a risolverli, come si dice, a caso, ma sarà un tempo molto lungo e quasi nessun successo.

In questo articolo parleremo di uno di questi misteri, ma per essere precisi – del quadrato magico. Analizziamo in dettaglio come risolvere il quadrato magico. 3 classe di un programma completo, naturalmente, va, ma forse non tutti capito o non ricordava.

Che cosa è questo mistero?

quadrato magico, o come si dice, magico – una tabella in cui il numero di colonne e righe della stessa, e sono tutti pieni di figure differenti. La sfida principale alle figure la quantità di verticale, orizzontale e diagonale dare lo stesso valore.

Oltre al quadrato magico, c'è anche un semi-magico. Ciò implica che la somma dei numeri ma la stessa verticalmente e orizzontalmente. quadrato magico "normale" solo nel caso in cui utilizzato per riempire i numeri naturali da unità.

C'è ancora una cosa come un quadrato magico simmetrica – questo è quando il valore della somma di due numeri è uguale, nel momento in cui sono disposti simmetricamente rispetto al centro.

E 'anche importante sapere che i quadrati possono essere di qualsiasi dimensione, oltre al 2 da 2 piazzare 1 su 1 è anche considerato essere magico, come tutte le condizioni sono soddisfatte, anche se costituito da un singolo numero.

Così, con la definizione che abbiamo letto, ora parliamo di come risolvere il quadrato magico. 3 classe curriculum è improbabile che spiegare tutto come dettagliato come questo articolo.

Quali sono le soluzioni

Quelle persone che sanno come risolvere il quadrato magico (3 class sa esattamente), subito dicono che le soluzioni sono solo tre, e ciascuno di essi è adatto per varie piazze, ma ancora non è possibile ignorare la quarta soluzione, vale a dire, il "random" . Dopo tutto, in qualche modo, v'è la possibilità che le persone ignoranti essere ancora in grado di risolvere questo enigma. Ma questo metodo abbiamo accantonato in una lunga scatola e passare direttamente alle formule e tecniche.

Il primo metodo. Quando la piazza è dispari

Questo metodo è adatto solo per risolvere un tale quadrato, che ha un numero dispari di cellule, per esempio, un 3 da 3 o 5 sul 5.

Quindi, in ogni caso, inizialmente deve trovare la costante magica. Questo numero, che si ottiene quando la quantità di numeri diagonalmente, verticalmente e orizzontalmente. Si è calcolato utilizzando la formula:

In questo esempio, consideriamo la piazza a tre a tre, la formula sarà simile modo (n – il numero di colonne):

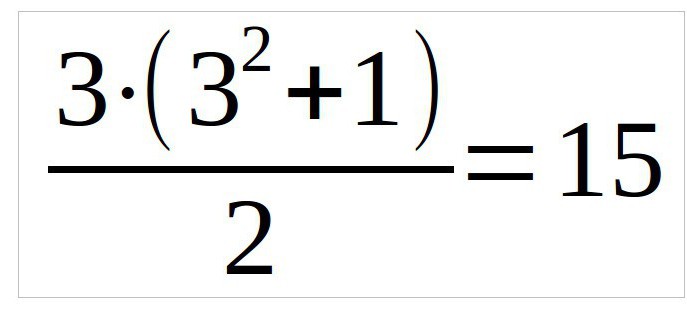
Così, abbiamo una piazza. La prima cosa da fare – è quello di inserire il numero uno al centro della prima linea dalla parte superiore. Tutti i numeri successivi devono essere collocati nelle stesse norme gabbia sulla diagonale.

Ma poi subito si pone la questione, come risolvere il quadrato magico? Grado 3 è improbabile che utilizzare questo metodo, e la maggior parte sarà un problema, come farlo in questo modo, se questo non è il cellulare? Per fare le cose giuste, è necessario utilizzare la vostra immaginazione e per finire lo stesso quadrato magico in alto e si scopre che il numero 2 sarà in esso nella cella in basso a destra. Quindi, nella nostra piazza entriamo i due nello stesso posto. Ciò significa che abbiamo bisogno di inserire i numeri in modo che insieme hanno dato un valore di 15.

I numeri successivi si inseriscono nello stesso modo. Cioè 3 sarà al centro della prima colonna. Ma 4 non sarà in grado di scrivere su questo principio, dal momento che la sua posizione è già un'unità. In questo caso, il numero 4 si trova sotto 3, e continuare. Cinque – al centro della piazza, 6 – nell'angolo superiore destro, 7 – per 6, 8 – in alto a sinistra e 9 – nel mezzo della linea di fondo.

Ora si sa come risolvere il quadrato magico. Demidov ha tenuto una classe 3, ma questo autore era un po 'compito più facile, ma conoscendo il modo per essere in grado di risolvere tali problemi. Ma questo, se un numero dispari di colonne. E cosa fare, se abbiamo, per esempio, un quadrato 4 per 4? Questo ulteriore nel testo.

Il secondo metodo. La quadratura del doppio parità

Quadrato doppia parità viene chiamato quello con il numero di colonne possono essere separati e 2 e 4. Ora consideriamo il quadrato 4 x 4.

Quindi, come risolvere il quadrato magico (grado 3, Demidov, Kozlov, sottile – ambientato nel manuale di matematica), quando il numero delle sue colonne è uguale a 4? E 'molto semplice. Più facile che nell'esempio precedente.

In primo luogo troviamo la costante magica utilizzando la stessa formula che è stato messo in l'ultima volta. In questo esempio, il numero è 34. Ora è necessario costruire i numeri tali che la somma del verticale, orizzontale e diagonale è lo stesso.

In primo luogo abbiamo bisogno di dipingere alcune delle cellule fare questo, è possibile matita o nella fantasia. Dipingere sopra tutti gli angoli, cioè la cella superiore sinistra e la destra superiore, inferiore sinistro e inferiore destro. Se il quadrato sarebbe 8 per 8, quindi non è necessario per dipingere una scatola in un angolo, e quattro, che misura 2 a 2.

Ora è necessario dipingere il centro della piazza, in modo che gli angoli degli angoli interessati cellule già ombreggiate. In questo esempio, si ottiene un quadrato al centro di un 2 a 2.

Ottenere il riempimento. Riempirà da sinistra a destra nell'ordine in cui si trovano le cellule, basta inserire il valore sarà nelle celle ombreggiate. Si scopre che l'angolo superiore sinistro 1 viene inserito nella destra – 4. quindi riempire il centrale 6, 7, e in seguito 10 e 11. Il basso a sinistra e destra 13 – 16. Crediamo la procedura di riempimento chiaro.

Le cellule rimanenti sono riempiti allo stesso modo, solo nell'ordine discendente. Questo perché quest'ultimo è stato inscritto figura 16, la parte superiore di un quadrato crei 15. Inoltre 14. Poi 12, 9 e così via, come mostrato in figura.

Ora che si conosce il secondo modo di risolvere il quadrato magico. Grado 3 concordano sul fatto che il quadrato della doppia parità è molto più facile da risolvere rispetto ad altri. Beh, ci rivolgiamo a quest'ultimo metodo.

La terza via. Al quadrato un singolo parità

Quadrato singolo parità viene chiamato il quadrato del numero di colonne che può essere diviso in due, ma non quattro. In questo caso, il quadrato di 6 6.

Quindi, si calcola la costante magica. È uguale a 111.

Ora dobbiamo quadrare visivamente divisa in quattro diverse quadrata di 3 per 3. 3 ha le dimensioni di quattro quadratino 3 in una grande 6 6. sinistra superiore è chiamato A, il basso a destra – B, in alto a destra – basso a sinistra e la C – D.

Ora è necessario per risolvere ogni piccolo quadrato, utilizzando il metodo originale che viene fornito in questo articolo. Risulta così che il quadrato A sono numeri da 1 a 9, nel V – dalle 10 alle 18, C – da 19 a 27 e D – da 28 a 36.

Una volta deciso tutti quattro quadrati, lavoro inizierà sulla A e D. Va nel quadrata A visivamente o con una matita diviso in tre celle, vale a dire, in alto a sinistra, in basso a sinistra, e il centro. In modo che i numeri assegnati – è 8, 5 e 4. Analogamente, è necessario identificare e Square D (35, 33, 31). Tutto ciò che rimane da fare è sostituire i numeri assegnati di piazzare D su A.

Ora che sapete l'ultimo modo in cui è possibile risolvere il quadrato magico. Grado 3 quadrato singolo di parità non ama più. Questo non è sorprendente, perché tutto ha presentato il più difficile.

conclusione

Dopo aver letto questo articolo, si è appreso come risolvere il quadrato magico. Grado 3 (Moreau – autore del libro di testo) offre attività simili con poche celle riempite. Si consideri il suo esempio non ha senso, come conoscere tutti e tre i metodi, si può facilmente risolvere tutti gli obiettivi proposti.