L'ipotesi di Riemann. Distribuzione dei numeri primi

Nel 1900 uno dei più grandi scienziati del secolo scorso, David Hilbert ha fatto un elenco composto da 23 problemi irrisolti della matematica. Il lavoro su di loro ha avuto un impatto enorme sullo sviluppo di questo campo della conoscenza umana. Dopo 100 anni nel Mathematical Institute di Clay ha presentato una lista di sette problemi, noti come gli obiettivi del Millennio. Per la decisione di ciascuno di essi è stato offerto il premio di $ 1 milione.

L'unico problema, che è stato tra i due elenchi di enigmi, per secoli, non ha dato riposo per gli scienziati, è diventato l'ipotesi di Riemann. Lei è ancora in attesa per la sua decisione.

informazioni biografiche Brief

Georg Friedrich Bernhard Riemann è nato nel 1826 ad Hannover, in una grande famiglia di un povero pastore, e ha vissuto solo 39 anni. Riuscì a pubblicare 10 articoli. Tuttavia, durante la vita di Riemann che considerava un successore del suo maestro Johann Gauss. A 25 anni giovane scienziato ha difeso la sua tesi "Fondamenti della teoria delle funzioni di una variabile complessa." In seguito ha formulato la sua ipotesi, che è diventato famoso.

numeri primi

La matematica è arrivata quando l'uomo ha imparato a contare. Poi è nata la prima idea di numeri, che poi processato da classificare. E 'stato osservato che alcuni di loro hanno proprietà comuni. In particolare, tra i numeri naturali m. E. Tali che sono stati utilizzati nel calcolo (numerazione) o il numero designato di elementi è stato assegnato un gruppo di tale che sono divisi da un solo e se stessi. Erano chiamati semplice. Un elegante dimostrazione del teorema insieme infinito di numeri dati da Euclide nei suoi "Elementi". Al momento, stiamo continuando la loro ricerca. In particolare, la più grande delle numerose noto ² 74207281 – 1.

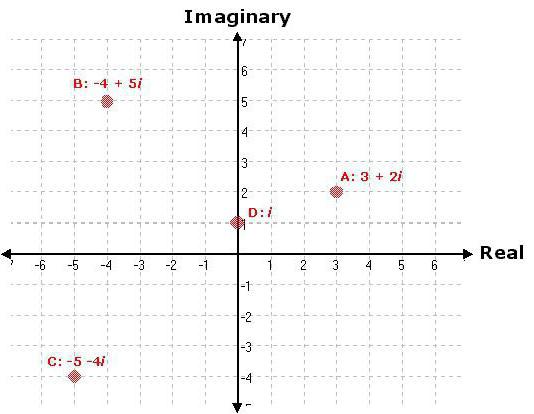
formula di Eulero

Insieme con la nozione di infiniti primi Euclide definita e il secondo teorema l'unica possibile fattorizzazione. In base ad esso un numero intero positivo è il prodotto di un solo set di numeri primi. Nel 1737, il grande matematico tedesco Leonhard Euler espresso prima del teorema di Euclide sulla infinità della formula mostrata sotto.

Si chiama la funzione zeta, dove s – una costante e p è tutto valori semplici. Da direttamente seguita e l'approvazione della unicità della espansione di Euclide.

funzione zeta di Riemann

La formula di Eulero a ben guardare è davvero notevole, come dato dal rapporto tra il semplice e interi. Dopo tutto, nel suo lato sinistro sono moltiplicati infinite espressioni che dipendono solo semplici, e nella giusta quantità è associato a tutti gli interi positivi.

Riemann ha continuato Euler. Al fine di trovare il bandolo della matassa della distribuzione dei numeri, si propone di definire la formula sia per la variabile reale e complessa. Era lei che in seguito divenne noto come la funzione zeta di Riemann. Nel 1859 lo scienziato ha pubblicato un articolo intitolato "Sul numero di numeri primi che non superano un valore predeterminato", che riassume tutte le loro idee.

Riemann ha proposto l'uso di un certo numero di Eulero, convergente per tutte le s reali> 1. Se la stessa formula per s complessi, allora la serie converge per qualsiasi valore della variabile con la parte reale è maggiore di 1. Riemann utilizzato il prolungamento analitico della procedura ampliando la definizione di zeta (s) per tutti i numeri complessi, ma "lanciare" unità. Non era possibile, perché se s = 1 funzione zeta tende a infinito.

senso pratico

La domanda sorge spontanea: che cosa è interessante e importante funzione zeta, che è cruciale nel lavoro di Riemann sulla ipotesi nulla? Come sapete, in questo momento non si trova un semplice schema che descrive la distribuzione dei numeri primi tra i naturale. Riemann grado di rilevare che il numero di pi (x) di numeri primi, che non sono superiori a x, è espressa dalla distribuzione di banale funzione di azzeramento zeta. Inoltre, l'ipotesi di Riemann è una condizione necessaria per dimostrare valutazioni temporanee di alcuni algoritmi crittografici.

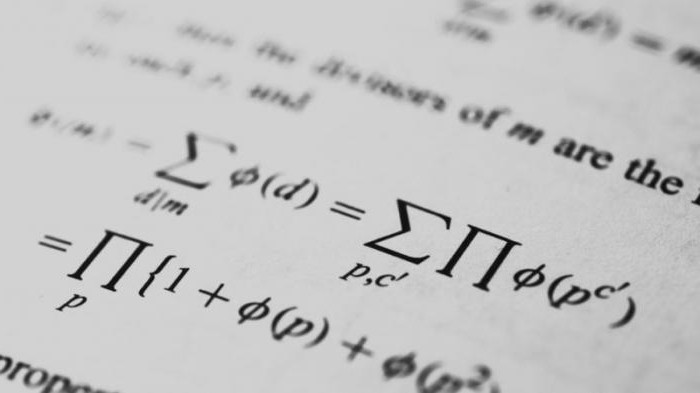
L'ipotesi di Riemann

Una delle prime formulazioni di questo problema matematico, non provata fino ad oggi, è: banale funzione zeta 0 – numeri complessi con parte reale pari a ½. In altre parole, essi sono disposti su una linea retta Re s = ½.

C'è anche un'ipotesi di Riemann generalizzata, che è la stessa dichiarazione, ma per la generalizzazione delle zeta-funzioni, che sono chiamati il Dirichlet (vedi. Foto sotto) L-funzioni.

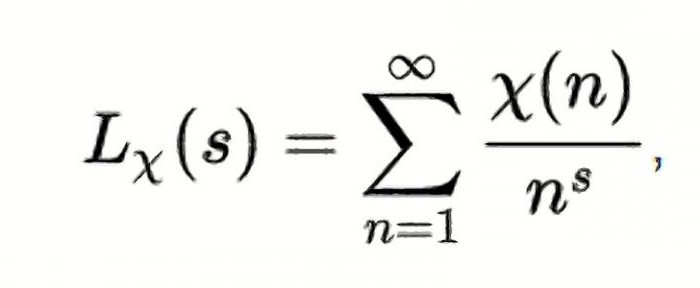
Nella formula χ (n) – un carattere numerico (mod k).

L'affermazione di Riemann è la cosiddetta ipotesi nulla, come si è verificato per la coerenza con i dati di esempio esistenti.

Come ho sostenuto Riemann

Nota matematico tedesco è stato originariamente formulato abbastanza casualmente. Il fatto è che in quel momento lo scienziato stava per dimostrare un teorema sulla distribuzione dei numeri primi, e in questo contesto, questa ipotesi non ha molto effetto. Tuttavia, il suo ruolo nell'affrontare le molte altre questioni è enorme. È per questo che l'ipotesi di Riemann per ora molti scienziati riconoscono l'importanza di problemi matematici non provati.

Come già accennato, per la prova della distribuzione dell'ipotesi piena Riemann non è necessario, e logicamente dimostrare che la parte reale di qualsiasi non banale zero della funzione zeta è tra 0 e 1. Questa proprietà implica che la somma di tutte le 0-m funzione zeta che appaiono nella formula esatta, – finita costante. Per grandi valori di x, tutto può essere perduto. L'unico membro della formula, che rimarrà invariata anche a velocità molto elevate x, x è lo stesso. Il resto dei termini complessi in confronto con essa asintoticamente scomparire. Pertanto, la somma ponderata tende a x. Questo fatto può essere considerato come prova della verità del teorema dei numeri primi. Così, gli zeri della funzione zeta di Riemann appare un ruolo particolare. È di dimostrare che questi valori non possono contribuire in modo significativo alla formula espansione.

seguaci di Riemann

La tragica morte di tubercolosi ha impedito lo scienziato portare alla fine logica del programma. Tuttavia, ha preso il testimone dal W-F. de la Vallée Poussin e Zhak Adamar. Indipendentemente l'uno dall'altro si erano ritirati teorema dei numeri primi. Hadamard e Poussin sono riusciti a dimostrare che tutte le funzioni 0 zeta non banale si trovano all'interno della banda critica.

Grazie al lavoro di questi scienziati, un nuovo ramo della matematica – la teoria analitica dei numeri. Più tardi, altri ricercatori hanno ricevuto un po 'la prova più primitivo del teorema stava lavorando a Roma. In particolare, Pal Erdös e Atle Selberg hanno aperto anche confermandosi altamente complessa catena di logica, non richiedono l'uso di analisi complessa. Tuttavia, a questo punto l'idea di Riemann di parecchi importanti teoremi hanno dimostrato, compreso il ravvicinamento delle numerose funzioni della teoria dei numeri. In relazione a questo nuovo lavoro Erdős e Atle Selberg praticamente qualsiasi cosa non sono interessate.

Una delle prove più semplice e bella del problema è stato trovato nel 1980 da Donald Newman. Esso si basa sul ben noto teorema di Cauchy.

Minacciata se l'ipotesi di Riemann è la base della crittografia moderna

La crittografia dei dati è emerso con la comparsa di personaggi, o meglio, si può essere considerato come il primo codice. Al momento, c'è una tendenza del tutto nuova della crittografia digitale, che è impegnata nello sviluppo di algoritmi di cifratura.

Semplice e "semisemplice" numero di m. E. Coloro che sono divisi solo in altre due numeri della stessa classe, sono la base di un sistema a chiave pubblica, noto come RSA. Ha una vasta applicazione. In particolare, è utilizzato nella generazione di una firma elettronica. Se parliamo in termini di "teiera" disponibili, l'ipotesi di Riemann afferma l'esistenza del sistema della distribuzione dei numeri primi. Così, ha ridotto significativamente la resistenza di chiavi crittografiche, che determinano la sicurezza delle transazioni online in e-commerce.

Altri problemi matematici irrisolti

Articolo completo vale la pena di dedicare qualche parola ad altri compiti del millennio. Questi includono:

• La parità di classi P e NP. Il problema è formulato come segue: se una risposta positiva ad una determinata questione viene verificata in tempo polinomiale, allora è vero che lui stesso la risposta a questa domanda si può trovare in fretta?
• Hodge congetture. In termini semplici può essere indicato come segue: per alcuni tipi di collettori algebriche proiettive (spazi) cicli Hodge sono combinazioni di oggetti che hanno un'interpretazione geometrica, cioè cicli algebrici …
• congettura di Poincaré. E 'l'unica provata al momento i problemi del millennio. In base ad esso qualsiasi oggetto tridimensionale avente proprietà specifiche della sfera 3-dimensionale, la sfera deve essere accurata alla deformazione.
• Approvazione del quantum teoria di Yang – Mills. Dobbiamo dimostrare che la teoria quantistica, formulata per questi scienziati di R ⁴ esiste ed è difetto 0-massa per qualsiasi semplice calibrazione di un gruppo compatto G.
• L'ipotesi della Birch – Swinnerton-Dyer. Questo è un altro problema che è rilevante alla crittografia. Essa riguarda le curve ellittiche.
• Il problema dell'esistenza e la morbidezza delle soluzioni delle equazioni di Navier – Stokes.

Ora sapete l'ipotesi di Riemann. In termini semplici, abbiamo formulato e alcuni degli altri obiettivi del millennio. Il fatto che essi saranno risolti o è accertato che non hanno nessuna soluzione – è una questione di tempo. E questo è improbabile che dover aspettare troppo a lungo, come la matematica sono sempre più utilizzando la potenza di calcolo dei computer. Tuttavia, non tutto è soggetto a l'arte e per risolvere i problemi scientifici richiede in primo luogo l'intuizione e la creatività.